18.2 Abstract syntax trees
Expressions are also called abstract syntax trees (ASTs) because the structure of code is hierarchical and can be naturally represented as a tree. Understanding this tree structure is crucial for inspecting and modifying expressions (i.e. metaprogramming).
18.2.1 Drawing
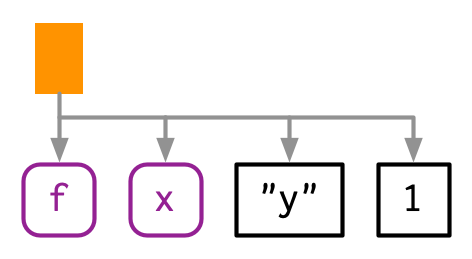
We’ll start by introducing some conventions for drawing ASTs, beginning with a simple call that shows their main components: f(x, "y", 1). I’ll draw trees in two ways59:
By “hand” (i.e. with OmniGraffle):
With
lobstr::ast():lobstr::ast(f(x, "y", 1)) #> █─f #> ├─x #> ├─"y" #> └─1
Both approaches share conventions as much as possible:
The leaves of the tree are either symbols, like
fandx, or constants, like1or"y". Symbols are drawn in purple and have rounded corners. Constants have black borders and square corners. Strings and symbols are easily confused, so strings are always surrounded in quotes.The branches of the tree are call objects, which represent function calls, and are drawn as orange rectangles. The first child (
f) is the function that gets called; the second and subsequent children (x,"y", and1) are the arguments to that function.
Colours will be shown when you call ast(), but do not appear in the book for complicated technical reasons.
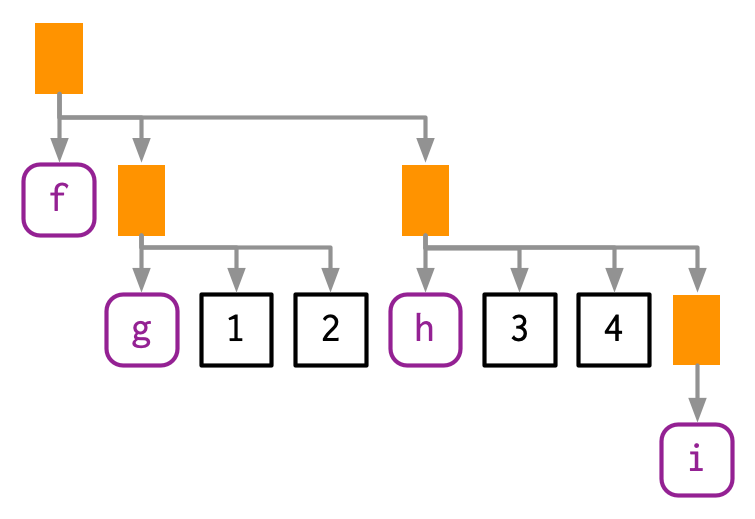
The above example only contained one function call, making for a very shallow tree. Most expressions will contain considerably more calls, creating trees with multiple levels. For example, consider the AST for f(g(1, 2), h(3, 4, i())):
lobstr::ast(f(g(1, 2), h(3, 4, i())))
#> █─f
#> ├─█─g
#> │ ├─1
#> │ └─2
#> └─█─h
#> ├─3
#> ├─4
#> └─█─iYou can read the hand-drawn diagrams from left-to-right (ignoring vertical position), and the lobstr-drawn diagrams from top-to-bottom (ignoring horizontal position). The depth within the tree is determined by the nesting of function calls. This also determines evaluation order, as evaluation generally proceeds from deepest-to-shallowest, but this is not guaranteed because of lazy evaluation (Section 6.5). Also note the appearance of i(), a function call with no arguments; it’s a branch with a single (symbol) leaf.
18.2.2 Non-code components
You might have wondered what makes these abstract syntax trees. They are abstract because they only capture important structural details of the code, not whitespace or comments:
ast(
f(x, y) # important!
)
#> █─f
#> ├─x
#> └─yThere’s only one place where whitespace affects the AST:
lobstr::ast(y <- x)
#> █─`<-`
#> ├─y
#> └─x
lobstr::ast(y < -x)
#> █─`<`
#> ├─y
#> └─█─`-`
#> └─x18.2.3 Infix calls
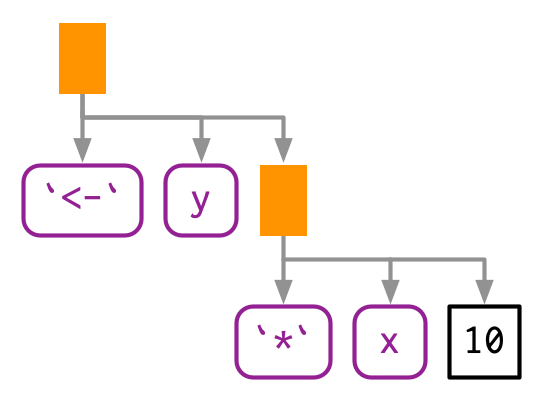
Every call in R can be written in tree form because any call can be written in prefix form (Section 6.8.1). Take y <- x * 10 again: what are the functions that are being called? It is not as easy to spot as f(x, 1) because this expression contains two infix calls: <- and *. That means that these two lines of code are equivalent:
y <- x * 10
`<-`(y, `*`(x, 10))And they both have this AST60:
lobstr::ast(y <- x * 10)
#> █─`<-`
#> ├─y
#> └─█─`*`
#> ├─x
#> └─10There really is no difference between the ASTs, and if you generate an expression with prefix calls, R will still print it in infix form:
expr(`<-`(y, `*`(x, 10)))
#> y <- x * 10The order in which infix operators are applied is governed by a set of rules called operator precedence, and we’ll use lobstr::ast() to explore them in Section 18.4.1.
18.2.4 Exercises
Reconstruct the code represented by the trees below:
#> █─f #> └─█─g #> └─█─h #> █─`+` #> ├─█─`+` #> │ ├─1 #> │ └─2 #> └─3 #> █─`*` #> ├─█─`(` #> │ └─█─`+` #> │ ├─x #> │ └─y #> └─zDraw the following trees by hand and then check your answers with
lobstr::ast().f(g(h(i(1, 2, 3)))) f(1, g(2, h(3, i()))) f(g(1, 2), h(3, i(4, 5)))What’s happening with the ASTs below? (Hint: carefully read
?"^".)lobstr::ast(`x` + `y`) #> █─`+` #> ├─x #> └─y lobstr::ast(x ** y) #> █─`^` #> ├─x #> └─y lobstr::ast(1 -> x) #> █─`<-` #> ├─x #> └─1What is special about the AST below? (Hint: re-read Section 6.2.1.)
lobstr::ast(function(x = 1, y = 2) {}) #> █─`function` #> ├─█─x = 1 #> │ └─y = 2 #> ├─█─`{` #> └─<inline srcref>What does the call tree of an
ifstatement with multipleelse ifconditions look like? Why?
For more complex code, you can also use RStudio’s tree viewer which doesn’t obey quite the same graphical conventions, but allows you to interactively explore large ASTs. Try it out with
View(expr(f(x, "y", 1))).↩︎The names of non-prefix functions are non-syntactic so I surround them with
``, as in Section 2.2.1.↩︎