18.4 Parsing and grammar
We’ve talked a lot about expressions and the AST, but not about how expressions are created from code that you type (like "x + y"). The process by which a computer language takes a string and constructs an expression is called parsing, and is governed by a set of rules known as a grammar. In this section, we’ll use lobstr::ast() to explore some of the details of R’s grammar, and then show how you can transform back and forth between expressions and strings.
18.4.1 Operator precedence
Infix functions introduce two sources of ambiguity65. The first source of ambiguity arises from infix functions: what does 1 + 2 * 3 yield? Do you get 9 (i.e. (1 + 2) * 3), or 7 (i.e. 1 + (2 * 3))? In other words, which of the two possible parse trees below does R use?
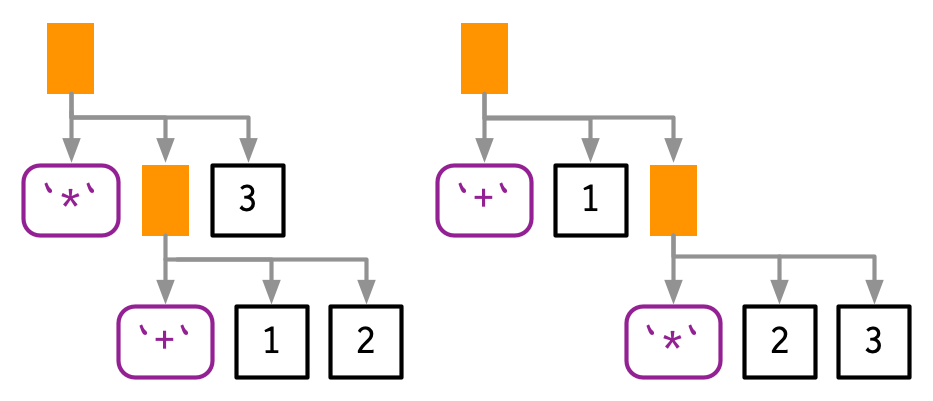
Programming languages use conventions called operator precedence to resolve this ambiguity. We can use ast() to see what R does:
lobstr::ast(1 + 2 * 3)
#> █─`+`
#> ├─1
#> └─█─`*`
#> ├─2
#> └─3Predicting the precedence of arithmetic operations is usually easy because it’s drilled into you in school and is consistent across the vast majority of programming languages.
Predicting the precedence of other operators is harder. There’s one particularly surprising case in R: ! has a much lower precedence (i.e. it binds less tightly) than you might expect. This allows you to write useful operations like:
lobstr::ast(!x %in% y)
#> █─`!`
#> └─█─`%in%`
#> ├─x
#> └─yR has over 30 infix operators divided into 18 precedence groups. While the details are described in ?Syntax, very few people have memorised the complete ordering. If there’s any confusion, use parentheses!
lobstr::ast((1 + 2) * 3)
#> █─`*`
#> ├─█─`(`
#> │ └─█─`+`
#> │ ├─1
#> │ └─2
#> └─3Note the appearance of the parentheses in the AST as a call to the ( function.
18.4.2 Associativity
The second source of ambiguity is introduced by repeated usage of the same infix function. For example, is 1 + 2 + 3 equivalent to (1 + 2) + 3 or to 1 + (2 + 3)? This normally doesn’t matter because x + (y + z) == (x + y) + z, i.e. addition is associative, but is needed because some S3 classes define + in a non-associative way. For example, ggplot2 overloads + to build up a complex plot from simple pieces; this is non-associative because earlier layers are drawn underneath later layers (i.e. geom_point() + geom_smooth() does not yield the same plot as geom_smooth() + geom_point()).
In R, most operators are left-associative, i.e. the operations on the left are evaluated first:
lobstr::ast(1 + 2 + 3)
#> █─`+`
#> ├─█─`+`
#> │ ├─1
#> │ └─2
#> └─3There are two exceptions: exponentiation and assignment.
lobstr::ast(2^2^3)
#> █─`^`
#> ├─2
#> └─█─`^`
#> ├─2
#> └─3
lobstr::ast(x <- y <- z)
#> █─`<-`
#> ├─x
#> └─█─`<-`
#> ├─y
#> └─z18.4.3 Parsing and deparsing
Most of the time you type code into the console, and R takes care of turning the characters you’ve typed into an AST. But occasionally you have code stored in a string, and you want to parse it yourself. You can do so using rlang::parse_expr():
x1 <- "y <- x + 10"
x1
#> [1] "y <- x + 10"
is.call(x1)
#> [1] FALSE
x2 <- rlang::parse_expr(x1)
x2
#> y <- x + 10
is.call(x2)
#> [1] TRUEparse_expr() always returns a single expression. If you have multiple expression separated by ; or \n, you’ll need to use rlang::parse_exprs(). It returns a list of expressions:
x3 <- "a <- 1; a + 1"
rlang::parse_exprs(x3)
#> [[1]]
#> a <- 1
#>
#> [[2]]
#> a + 1If you find yourself working with strings containing code very frequently, you should reconsider your process. Read Chapter 19 and consider whether you can generate expressions using quasiquotation more safely.
The base equivalent to parse_exprs() is parse(). It is a little harder to use because it’s specialised for parsing R code stored in files. You need to supply your string to the text argument and it returns an expression vector (Section 18.6.3). I recommend turning the output into a list:
as.list(parse(text = x1))
#> [[1]]
#> y <- x + 10
The inverse of parsing is deparsing: given an expression, you want the string that would generate it. This happens automatically when you print an expression, and you can get the string with rlang::expr_text():
z <- expr(y <- x + 10)
expr_text(z)
#> [1] "y <- x + 10"Parsing and deparsing are not perfectly symmetric because parsing generates an abstract syntax tree. This means we lose backticks around ordinary names, comments, and whitespace:
cat(expr_text(expr({
# This is a comment
x <- `x` + 1
})))
#> {
#> x <- x + 1
#> }Be careful when using the base R equivalent, deparse(): it returns a character vector with one element for each line. Whenever you use it, remember that the length of the output might be greater than one, and plan accordingly.
18.4.4 Exercises
R uses parentheses in two slightly different ways as illustrated by these two calls:
f((1)) `(`(1 + 1)Compare and contrast the two uses by referencing the AST.
=can also be used in two ways. Construct a simple example that shows both uses.Does
-2^2yield 4 or -4? Why?What does
!1 + !1return? Why?Why does
x1 <- x2 <- x3 <- 0work? Describe the two reasons.Compare the ASTs of
x + y %+% zandx ^ y %+% z. What have you learned about the precedence of custom infix functions?What happens if you call
parse_expr()with a string that generates multiple expressions? e.g.parse_expr("x + 1; y + 1")What happens if you attempt to parse an invalid expression? e.g.
"a +"or"f())".deparse()produces vectors when the input is long. For example, the following call produces a vector of length two:expr <- expr(g(a + b + c + d + e + f + g + h + i + j + k + l + m + n + o + p + q + r + s + t + u + v + w + x + y + z)) deparse(expr)What does
expr_text()do instead?pairwise.t.test()assumes thatdeparse()always returns a length one character vector. Can you construct an input that violates this expectation? What happens?
This ambiguity does not exist in languages with only prefix or postfix calls. It’s interesting to compare a simple arithmetic operation in Lisp (prefix) and Forth (postfix). In Lisp you’d write
(* (+ 1 2) 3)); this avoids ambiguity by requiring parentheses everywhere. In Forth, you’d write1 2 + 3 *; this doesn’t require any parentheses, but does require more thought when reading.↩︎